Visualising Matrices and Affine Transformations With Python

02-Jan-2015

Here, we visualise matrix linear and affine transformations to set the foundation in understanding more awesome computer vision techniques (still a learning process for me).

There is an assumed knowledge of the core mathematical concepts in matrices and vectors. If a refresher is needed, I highly recommend Khan Academy’s Precalculus course.

I also recommend Khan Academy’s Linear Algebra course for further learning.

Linear vs Affine transform

Quick distinction. Linear transformations are fixed around the origin (scaling, rotating, skewing). Affine transformations are a linear function followed by a translation.

Visualising a matrix

Points in 2D space can be written as (3, 13), (5, 15). A set of 2D vectors can be written in a matrix as $\begin{bmatrix}
3 & 5 \\
13 & 15
\end{bmatrix}$ with each column representing a data point.
So, matrix $P$ = $\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0
\end{bmatrix}$ consists of 4 points. Lets plot it in Python.

First, the libraries:


import numpy as np
import matplotlib.pyplot as plt

I’m going to draw a line between the points but you should picture the line as a row of many points. Heres the function to plot the matrix that will be reused throughout this post:


def plot_points(matrix, ls='--', lw=1.2, colors=None):
  x_points, y_points = matrix
  size = len(x_points)
  colors = ['red', 'blue', 'orange', 'green'] if not None else colors
  for i in range(size):
    plt.plot(x_points[i], y_points[i], color=colors[i], marker='o')
    plt.plot([x_points[i], x_points[(i+1) % size]], 
             [y_points[i], y_points[(i+1) % size]], 
             color=colors[i], 
             linestyle=ls, linewidth=lw)

Now, we plot our matrix, $P$.


x_points = np.array([0, 0, 20, 20])
y_points = np.array([0, 20, 20, 0])
matrix = np.array([x_points, y_points])
colors = ['red', 'blue', 'orange', 'green']
size = len(x_points)
plot_points(matrix, colors)
plt.ylim([-5,25])
plt.xlim([-5,25])
plt.axes().set_aspect('equal')
plt.show()

And our matrix $P$ = $\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0
\end{bmatrix}$ can be visualised as the corners of a square. Remember to view the lines as a bunch of points.

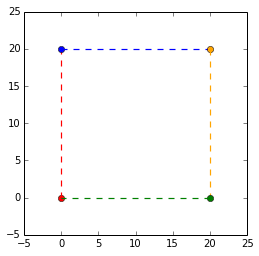
Identity matrix

Multiplying a matrix with the identity matrix does nothing to the matrix.
That is, $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
\begin{bmatrix} 3 \\ 13 \end{bmatrix} = \begin{bmatrix} 3 \\ 13 \end{bmatrix}$. Each column in the indentity matrix are called basis vectors (linearly independent and equations solve for 0). These will be super useful in deriving and visualising the transformation matrices.

Scaling

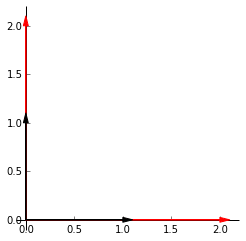
Lets say we want to scale our points by 2. The plot on the left shows the identity matrix in black and our end goal in red. Heres the github gist for the plot. The first vector along the _x_-axis, $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ has to be multipled by 2 to get to $\begin{bmatrix} 2 \\ 0 \end{bmatrix}$. The same is applied to the second vector along the _y_-axis. Our end matrix is $\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$.

To generalise, we can multiply a matrix by $\begin{bmatrix} k1 & 0 \\ 0 & k2 \end{bmatrix}$ to achieve scaling in 2D space. $k1$ and $k2$ can be the same or different to obtain different scalings in the different dimensions.

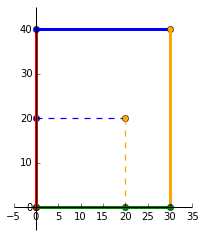
Lets try scaling our matrix $P$ by multiplying it with the matrix:
$\begin{bmatrix}
1.5 & 0 \\
0 & 2
\end{bmatrix}$ As expected, we can see that the original square (dashed lines) has been scaled by 1.5 in the positive _x_ direction and scaled by 2 in the positive _y_ direction.

The resultant matrix is:
$\begin{bmatrix}
1.5 & 0 \\
0 & 2
\end{bmatrix} \times
\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0
\end{bmatrix} =
\begin{bmatrix}
0 & 0 & 30 & 30\\
0 & 40 & 40 & 0
\end{bmatrix}$

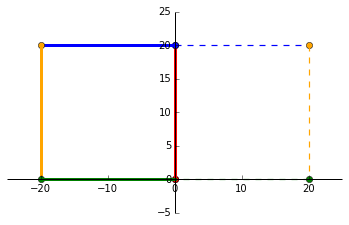
Reflecting

We can reflect the points along the _y_-axis by multiplying all _x_ coordinates by -1. So, $(1, 1)$ becomes $(-1, 1)$. That means we can multiply a matrix by $\begin{bmatrix}
-1 & 0 \\
0 & 1
\end{bmatrix}$ and it’ll mirror along the _y_-axis. And the visuals!

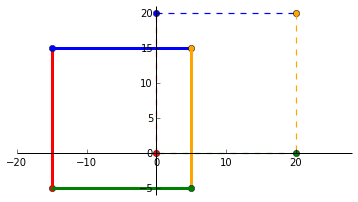
Skewing

Lets skew the identity matrix by +50%. The vector along the _x_-axis stays the same while the vector along the _y_-axis shifts _k_ = 0.5 to the right. Our resultant matrix is now $\begin{bmatrix}
1 & 0.5 \\
0 & 1
\end{bmatrix}$ and a skewing transformation matrix can be generalised as $\begin{bmatrix}
1 & k \\
0 & 1
\end{bmatrix}$.

So, doing
$\begin{bmatrix}
1 & 0.5 \\
0 & 1
\end{bmatrix} \times
\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0
\end{bmatrix}$
will skew $P$ by 50%.

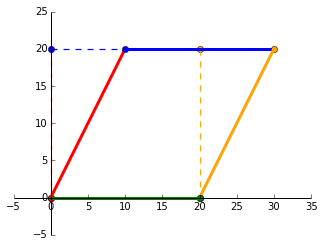
Rotating

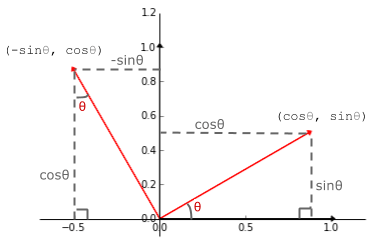
My favourite linear transformation. Using the trusty SOH CAH TOA acronym, we can see that
(1, 0) on the _x_-axis lands on $(cos \theta, sin \theta)$ and
(0, 1) on the _y_-axis lands on $(-sin \theta, cos \theta)$ when rotated by positive $\theta$.

Thus, our rotating transformation matrix has the general form: $\begin{bmatrix}
cos \theta & -sin \theta \\
sin \theta & cos \theta
\end{bmatrix}$.

Lets plot $P$ when it is rotated by $-30^\circ$. Note the change in negative $sin$ for clockwise rotation. Our matrices involved in this transformation are:

$\begin{bmatrix}
0.866 & 0.5 \\
-0.5 & 0.866
\end{bmatrix} \times
\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0
\end{bmatrix} =
\begin{bmatrix}
0 & 10 & 27.32 & 17.32\\
0 & 17.32 & 7.32 & -10
\end{bmatrix}$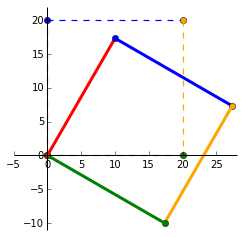

Translating

Lastly, the affine transform to translate a matrix. To do this, we need to represent a 2-vector $(x, y)$ to a 3-vector $(x, y, 1)$. A translation matrix has the form $\begin{bmatrix}
1 & 0 & t1 \\
0 & 1 & t2 \\
0 & 0 & 1
\end{bmatrix}$ where $t1$ and $t2$ translates a vector in the _x_ and _y_ direction. Lets translate $P$ to the left by 75% and downwards by 25%. Unlike the linear transformations where the scalars are multipliers, the affine scalars specify the distance to be translated.

$\begin{bmatrix}
1 & 0 & -15 \\
0 & 1 & -5 \\
0 & 0 & 1
\end{bmatrix} \times
\begin{bmatrix}
0 & 0 & 20 & 20\\
0 & 20 & 20 & 0 \\
1 & 1 & 1 & 1
\end{bmatrix}$


A = np.matrix([[1, 0, -0.75*20], [0, 1, -0.25*20], [0, 0, 1]]) 
P = np.matrix([[0, 0, 20, 20], [0, 20, 20, 0], [1, 1, 1, 1]])   
translated_matrix = A*P

translated_matrix:

matrix([[ -0.75,  -0.75,  19.25,  19.25],
        [ -0.25,  19.75,  19.75,  -0.25],
        [  1.  ,   1.  ,   1.  ,   1.  ]])

Transformation matrix

Heres a summary of the transformation matrices (courtesy of wikipedia). Notice that a 2x2 linear transformation matrix becomes a 3x3 transformation matrix by padding it with 0s and a 1 at the bottom-right corner.

So, for vectors in 3D ($\mathbb{R}^3$) space, its linear transformation matrix is 3x3 and its affine transformation matrix (usually called without the affine) is 4x4 and so on for higher dimensions.

Alyssa Quek

data science